Selección de modelos y evaluación#

  • Cómo medimos si un modelo está “bien” entrenado

  • Flujo general de trabajo en ML

  • Basado en ESL parte 7 Selección y evaluación de modelos.

Versión b.1#

El notebook lo puedo modificar, esta versión es la b.1 a 14/06/2024 a las 2pm de Caracas.

Aprendizaje Automático [UCV]#

Evaluación de modelos#

Nuestro objetivo siempre ha sido conseguir una función \(f\) pero, hasta el momento, no hemos hablado sobre medir qué tan buena es.

El objetivo principal si bien es conseguir una \(f\) debe cambiar a una \(f\) buena. Intuitivamente, una función \(f\) funciona bien si es capaz de generalizar sobre datos independientes o no vistos.

Resumen de dónde estamos#

  1. Variable objetivo \(Y \in \mathbb{R}\),

  2. Un vector de entradas \(X \in \mathbb{R}^p\)

  3. Un modelo de predicción \(\hat{f}(X)\) que se ha estimado a partir de un conjunto de entrenamiento \(\mathcal{T}\).

  4. La función de pérdida para medir errores entre \(Y\) y \(\hat{f}(X)\) se denota por \(L(Y, \hat{f}(X))\).

Las selecciones típicas son: $\( L(Y, \hat{f}(X))= \begin{cases}(Y-\hat{f}(X))^2 & \text { squared error } \\ |Y-\hat{f}(X)| & \text { absolute error. }\end{cases} \)$

Definiciones#

Error de prueba#

También conocido como error de generalización, es el error de predicción sobre una muestra de prueba independiente. $\( \operatorname{Err}_{\mathcal{T}}=\mathrm{E}[L(Y, \hat{f}(X)) \mid \mathcal{T}] \)$

  1. \(X\) como \(Y\) se extraen aleatoriamente de su distribución conjunta (población).

  2. Aquí el conjunto de entrenamiento \(\mathcal{T}\) es fijo

  3. El error de prueba se refiere al error de este conjunto de entrenamiento específico.

Error de entrenamiento#

El error de entrenamiento, es el promedio de la función de pérdida sobre los datos de entrenamiento \(\mathcal{T}\). $\( \overline{\mathrm{err}}=\frac{1}{N} \sum_{i=1}^N L\left(y_i, \hat{f}\left(x_i\right)\right) . \)$

Error de predicción esperado#

Error de predicción esperado (o error de prueba esperado) $\( \operatorname{Err}=\mathrm{E}[L(Y, \hat{f}(X))]=\mathrm{E}\left[\operatorname{Err}_{\mathcal{T}}\right ] \)$

Tenga en cuenta que esta esperanza promedia todo lo que es aleatorio, incluida la aleatoriedad en el conjunto de entrenamiento que produjo \(\hat{f}\).

Veamos esto en la siguiente figura

image.png

El objetivo#

Aún cuando \(\operatorname{Err}\) (Error de prueba esperado) es mucho mejor desde el punto de vista estadístico. Nuestro objetivo es estimar \(\operatorname{Err}_{\mathcal{T}}\) (error de prueba)

Por qué?

En general, teóricamente se le da importancia al Error de predicción esperado ()

Qué sucede con los parámetros de ajuste (tuning) (\(\lambda\))?#

Normalmente, nuestro modelo tendrá un parámetro o parámetros de ajuste \(\alpha\) y, por lo tanto, podemos escribir nuestras predicciones como $\(\hat{f}_\lambda(x)\)$

El parámetro de ajuste varía la complejidad de nuestro modelo y deseamos encontrar el valor de \(\beta\) que minimice el error, es decir, que produzca el mínimo de la curva de error de prueba promedio en la Figura.

Selección y evaluación de modelos#

  1. Selección de modelo: estimar el rendimiento de diferentes modelos para elegir el mejor.

  2. Evaluación del modelo: habiendo elegido un modelo final, estimando su error de predicción (error de generalización) sobre nuevos datos.

Pipeline general de evaluación#

  1. Separación entrenamiento y prueba (Train-Test split)

  2. Separación entrenamiento, prueba y validación(Train-Validation-Test split)

  3. Validación cruzada (Cross-validation): Permite evaluar el rendimiento de un estimador.

  4. Afinación de hiper-parámetros (hyper-parameters tunig): Métodos para conseguir buenos hiper-parámetros que no afectan los estimadores!

  5. Métricas y puntuación de métodos (metrics and scoring)

  6. Curvas de validación: Validation curves: plotting scores to evaluate models

1. Separación entrenamiento | prueba#

traintest.drawio.png

import numpy as np
from sklearn.model_selection import train_test_split

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 2
      1 import numpy as np
----> 2 from sklearn.model_selection import train_test_split

ModuleNotFoundError: No module named 'sklearn'

https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html

X, y = np.arange(20).reshape((10, 2)), range(10)

len(y)

20

X.shape

(10, 2)

X

array([[ 0,  1],
       [ 2,  3],
       [ 4,  5],
       [ 6,  7],
       [ 8,  9],
       [10, 11],
       [12, 13],
       [14, 15],
       [16, 17],
       [18, 19]])

 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1, shuffle=True)

?train_test_split

X_train

array([[ 0,  1],
       [ 6,  7],
       [ 2,  3],
       [14, 15],
       [16, 17],
       [10, 11]])

X_train

array([[ 0,  1],
       [ 2,  3],
       [ 4,  5],
       [ 6,  7],
       [ 8,  9],
       [10, 11]])

X_train

array([[14, 15],
       [ 4,  5],
       [18, 19],
       [ 8,  9],
       [ 6,  7],
       [12, 13]])

X_test

array([[16, 17],
       [ 2,  3],
       [10, 11],
       [ 0,  1]])

y_test

[8, 1, 5, 0]

y_train

[7, 2, 9, 4, 3, 6]

y_test

[13, 39, 30, 45, 17, 48, 26, 25, 32, 19, 12, 4, 37, 8, 3, 6, 41]

X_train

array([[92, 93],
       [94, 95],
       [30, 31],
       [18, 19],
       [32, 33],
       [48, 49],
       [68, 69],
       [62, 63],
       [ 0,  1],
       [88, 89],
       [54, 55],
       [66, 67],
       [10, 11],
       [58, 59],
       [22, 23],
       [72, 73],
       [ 2,  3],
       [42, 43],
       [ 4,  5],
       [86, 87],
       [70, 71],
       [46, 47],
       [80, 81],
       [20, 21],
       [44, 45],
       [36, 37],
       [98, 99],
       [40, 41],
       [14, 15],
       [84, 85],
       [28, 29],
       [56, 57],
       [76, 77]])

 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, random_state=42)

X_train.shape

(30, 2)

Entrenamiento en el conjunto de prueba

data leak

2. Separación entrenamiento | validación | prueba#

validation.drawio.png

3. Validación cruzada (cross-validation)#

image.png

3.1 Tipos de validación cruzada#

Vamos a tener 3 criterios para crear los folds

  1. Queremos conservar el orden de los índices?

  2. Queremos mantener la proporción de las clases?

  3. Queremos respetar los grupos entre el proceso generador de datos?

Dependiendo de las respuestas a las 3 preguntas, podremos decidir la mejor alternativa.

Existen muchas maneras, en la sección Cross validation de Scikit-Learn explican la mayoría. En nuestro curso, nos vamos a enfocar en las preguntas 1 y 2. A menos que sea indicado, asumimos siempre que la respuesta a 1. es no. Para el caso donde 1. es no ver la sección TimeSeriesSplit.

Para el caso donde 1. es no y además no consideramos 3., en general nos quedan 2 casos posibles

3.2 Validación cruzada: KFold#

Kfold divide los datos de entrenamiento en \(K\) pedazos. Para cada split, entrenamos nuestro algoritmo y nuestro estimador final será el average de los estimadores de cada split

image.png

import numpy as np
from sklearn.model_selection import KFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2])

kf = KFold(n_splits=3)
print(kf)
for i, (train_index, test_index) in enumerate(kf.split(X, y)):
  print(f"Fold {i}:")
  print(f"  Entrenamiento: índices={train_index}")
  print(f"  Prueba:  índices={test_index}")

KFold(n_splits=3, random_state=None, shuffle=False)
Fold 0:
  Entrenamiento: índices=[ 5  6  7  8  9 10 11 12 13]
  Prueba:  índices=[0 1 2 3 4]
Fold 1:
  Entrenamiento: índices=[ 0  1  2  3  4 10 11 12 13]
  Prueba:  índices=[5 6 7 8 9]
Fold 2:
  Entrenamiento: índices=[0 1 2 3 4 5 6 7 8 9]
  Prueba:  índices=[10 11 12 13]

Qué problema conseguimos en el fold 2?

3.3 Validación cruzada: StratifiedKFold#

En el caso de que la respuesta de la pregunta 2. sea si, buscamos respetar la proporción de clases dentro de cada fold

image.png

import numpy as np
from sklearn.model_selection import StratifiedKFold

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2])

X.shape

(14, 2)

skf = StratifiedKFold(n_splits=3)
print(skf)
for i, (train_index, test_index) in enumerate(skf.split(X, y)):
  print(f"Fold {i}:")
  print(f"  Entrenamiento: índices={train_index}")
  print(f"  Prueba:  índices={test_index}")

StratifiedKFold(n_splits=3, random_state=None, shuffle=False)
Fold 0:
  Entrenamiento: índices=[ 1  2  4  5  9 10 11 12 13]
  Prueba:  índices=[0 3 6 7 8]
Fold 1:
  Entrenamiento: índices=[ 0  2  3  5  6  7  8 12 13]
  Prueba:  índices=[ 1  4  9 10 11]
Fold 2:
  Entrenamiento: índices=[ 0  1  3  4  6  7  8  9 10 11]
  Prueba:  índices=[ 2  5 12 13]

Validación cruzada: StratifiedKFold#

3.4 Caso especial: series de tiempo#

En el caso de series de tiempo, al ser procesos estocásticos el orden de los datos importa. En cuyo caso, la representación es similar a la Figura debajo. Creamos conjuntos de entrenamiento y prueba conservando los índices de nuestros datos.

image.png

from sklearn.model_selection import TimeSeriesSplit

X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])

tscv = TimeSeriesSplit(n_splits=3)
print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
for train, test in tscv.split(X):
  print("%s %s" % (train, test))

TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
[0 1 2] [3]
[0 1 2 3] [4]
[0 1 2 3 4] [5]

https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.StratifiedKFold.html#sklearn.model_selection.StratifiedKFold

3.5 Usando pandas y numpy (sin scikit learn)#

import pandas as pd
import numpy as np

n, m = 25, 4

X, y = np.arange(n * m).reshape((n, m)), range(n)

X[0,1:]

array([1, 2, 3])

df = pd.DataFrame(
    data=X,    # Valores
    index=np.arange(n),    # 1st column as index
    columns=np.arange(m)
)

df.head()
0 1 2 3
0 0 1 2 3
1 4 5 6 7
2 8 9 10 11
3 12 13 14 15
4 16 17 18 19 
train, validate, test = np.split(df.sample(frac=1), [int(.6*len(df)), int(.8*len(df))])

validate
0 1 2 3
24 96 97 98 99
12 48 49 50 51
16 64 65 66 67
0 0 1 2 3
20 80 81 82 83 
train
0 1 2 3
13 52 53 54 55
7 28 29 30 31
6 24 25 26 27
11 44 45 46 47
4 16 17 18 19
10 40 41 42 43
3 12 13 14 15
2 8 9 10 11
18 72 73 74 75
14 56 57 58 59
21 84 85 86 87
19 76 77 78 79
1 4 5 6 7
5 20 21 22 23
17 68 69 70 71

4. Métricas para regresión#

4.1 Coficiente de determinación \(R^2\)#

Gráfico tomado de Coefficient of determination

image.png

\[R^2=1-\frac{\color{blue}{S S_{\mathrm{res}}}}{\color{red}{S S_{\mathrm{tot}}}}\]

De donde $\(\color{blue}{S S_{\mathrm{res}}} = \sum_i\left(y_i-f(x_i)\right)^2=\sum_i e_i^2 \)\( y \)\(\color{red}{S S_{\mathrm{tot}}} = S S_{\mathrm{tot}}=\sum_i\left(y_i-\bar{y}\right)^2 \)$

  1. Vean como el denominador es constante para todos los posibles modelos!

  2. Cuáles son los posibles valores de \(R^2\)

from sklearn.metrics import r2_score
import numpy as np

y_true = [1, 2, 3]
y_pred = [1, 2, 3]
r2_score(y_true, y_pred)

1.0

4.1.1 Intentemos nosotros#

1 - np.sum((np.array(y_pred)-np.array(y_true))**2)/ np.sum((np.array(y_true)-np.mean(y_true))**2)

-7.0

4.2 Coeficiente de correlación#

\[ r=\frac{\displaystyle \sum_{x \in X, y\in Y}\left(x-\bar{x}\right)\left(y-\bar{y}\right)}{\sqrt{\displaystyle \sum_{x \in X}\left(x-\bar{x}\right)^2 \sum_{y \in Y}\left(y-\bar{y}\right)^2}}\]

  1. Siendo \(\bar{x}\) y \(\bar{y}\) el average de los vectores \(X\) y \(Y\)

  2. \(r \in [-1, 1]\)

  3. 0 implica no correlación.

  4. \(1\) Implica correlación positiva

  5. \(-1\) Implica correlación negativa.

import scipy

Para nosotros, usamos que \(X\) y \(Y\) son las predicciones del modelo

y_true = [1, 2, 3, 4, 5, 6, 7, 8]
y_pred = [1, 5, 3, 3, 5, 6, -7, -5]

r, p = scipy.stats.pearsonr(y_true, y_pred)

r

-0.5484416125623885

p

0.15927063902456506

4.2.1 [Fuera de ML] Proba!!#

El parámetro \(p\) tiene que ver con constraste/test de hipótesis. Lo vimos (o debimos ver) en Probabilidades y estadística!

Parameters:

  1. x(N,) array_like Input array.

  2. y(N,) array_like Input array.

  3. alternative{‘two-sided’, ‘greater’, ‘less’}, optional Defines the alternative hypothesis. Default is ‘two-sided’. The following options are available:

  • ‘two-sided’: the correlation is nonzero

  • ‘less’: the correlation is negative (less than zero)

  • ‘greater’: the correlation is positive (greater than zero)

p

0.6801383015910456

4.2.2 Cuidado#

\(r\) es susceptible a valores extremos!!

y_true = [1, 2, 3, 4, 5, 6, 7, 8]
y_pred = [-1, -2, -3, -4, -5, -6, -7, -8]

r, p = scipy.stats.pearsonr(y_true, y_pred)

r

-0.9999999999999998

5. Métricas de clasificación#

5.1 Matriz de confusión para clasificación binaria#

Basamos nuestra tabla de interés en Precision and recall

image.png

5.2 Curvas ROC#

Calculemos las métricas para este caso

image.png

image.png

Movamos el umbral

image.png

Ahora, casos extremos

image.png

image.png

5.3 Análisis de curvas ROC#

image.png

image.png

5.4 Algoritmo de curvas ROC#

Sea scores el vector de salida del modelo de regresión para todos los \(x\)

  1. Entrenar modelo deseado con selección deseada.

  2. Ordenar scores de mayor a menor.

  3. Mover el umbral para cada elemento de scores y crear matriz de confusión.

  4. Almacenar TRP y TRN para cada umbral.

  5. Gráfico de curva de TRP y TRN

image.png

5.4.1 La métrica de ROC#

Cuál métrica creen sería idónea dadas las curvas?

En general, usaremos ROC AUC Score de scikit learn.

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score

X, y = load_breast_cancer(return_X_y=True)

clf = LogisticRegression(solver="liblinear", random_state=0).fit(X, y)
roc_auc_score(y, clf.predict_proba(X)[:, 1])

0.994767718408118

5.4.2 Cómo ver las curvas ROC?#

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import RocCurveDisplay, auc, roc_curve

y = y
pred = clf.predict_proba(X)[:, 1]
fpr, tpr, thresholds = roc_curve(y, pred)
roc_auc = auc(fpr, tpr)
display = RocCurveDisplay(fpr=fpr, tpr=tpr, roc_auc=roc_auc,
                                   estimator_name='example estimator')
display.plot()
plt.title("Curva ROC para breast cancer dataset")
plt.axis("square") # Por qué?
plt.show()
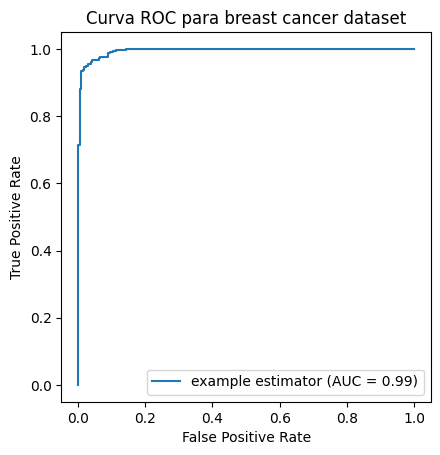
../../_images/3abf8802fd6d570fb78eb2fdd652ee8087540fad16049e663a9db1dacd84f648.png

5.5 Fuera de clasificación binaria#

5.2 Matriz de confusión con más de 2 clases#

Sin embargo, a nivel general la matriz tendrá dimensión \(m \times m\) siendo precisión la métrica estándar para todos los casos. Si \(Conf\) es la matriz de confusión entonces: $\(\text{Precisión} = \frac{tr(Conf)}{P+N} = \frac{\sum_{i \in \left[C \right]}Conf_{ii}}{P+N} \)$

6. Afinación de hiper parámetros#

from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler

from sklearn.datasets import load_breast_cancer

X, y = load_breast_cancer(return_X_y=True)

 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, random_state=42)

params = [{'knn__n_neighbors': [3, 5, 7, 9],
         'knn__weights': ['uniform', 'distance'],
         'knn__leaf_size': [15, 20]}]

knn_pipe = Pipeline([('mms', MinMaxScaler()),
                     ('knn', KNeighborsClassifier())])

gs_knn = GridSearchCV(knn_pipe,
                      param_grid=params,
                      scoring='accuracy',
                      cv=5)
gs_knn.fit(X_train, y_train)

GridSearchCV(cv=5,
             estimator=Pipeline(steps=[('mms', MinMaxScaler()),
                                       ('knn', KNeighborsClassifier())]),
             param_grid=[{'knn__leaf_size': [15, 20],
                          'knn__n_neighbors': [3, 5, 7, 9],
                          'knn__weights': ['uniform', 'distance']}],
             scoring='accuracy')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
gs_knn.best_params_

{'knn__leaf_size': 15, 'knn__n_neighbors': 9, 'knn__weights': 'distance'}

# find best model score
gs_knn.score(X_train, y_train)

1.0