from tldraw import TldrawWidget
t = TldrawWidget(width=1502, height = 700)
t
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 from tldraw import TldrawWidget
2 t = TldrawWidget(width=1502, height = 700)
3 t
ModuleNotFoundError: No module named 'tldraw'
from tldraw import TldrawWidget
t = TldrawWidget(width=1502, height = 700)
t
from tldraw import TldrawWidget
t = TldrawWidget(width=1502, height = 700)
t
from tldraw import TldrawWidget
t = TldrawWidget(width=1502, height = 700)
t
!pip install tldraw
Installing collected packages: psygnal, jedi, ipylab, anywidget, tldraw
Successfully installed anywidget-0.9.12 ipylab-1.0.0 jedi-0.19.1 psygnal-0.11.1 tldraw-2.0.14
Regresión logística#
Primer caso base de clasificación
Usaremos el modelo de regresión logística que se conecta con regresión
Versión b.1#
El notebook lo puedo modificar, esta versión es la v.1.0.0 a 29/05/2024 a las 1 p.m de Caracas.
Bibliografía#
Página 139-145 ISLP
Contacto#
Autor: Fernando Crema García
Contacto: fernando.cremagarcia@kuleuven.be; fernando.cremagarcia@esat.kuleuven.be
All of Statistics: A concise course in Statistical Inference
Larry Wasserman
Clasificación#
Recordemos que buscamos una función \(f\) sobre un conjunto de clases que podemos llamar \(C\) que es discreto y finito.
Color de ojo \(\in \text{marrón} ,\text{azul},\text{verde}\)
Dado un vector de características \(x \in X\) y una respuesta cualitativa \(y\) tomando valores en el conjunto \(\mathcal{C}\), la tarea de clasificación es construir una función \(f\) que podemos llamar \(C(x)\) que tome como entrada el vector de características \(x\) y predice su valor para \(y\); es decir, \(C(x) \in \mathcal{C}\).
Muchas veces estamos más interesados en estimar las probabilidades de que \(x\) pertenezca a cada categoría en \(\mathcal{C}\).
Clasificación Binaria#
Si \(|C|=2\) decimos que estamos en un escenario de clasificación binaria. Normalmente, los valores de \(C\) son \(\{-1, 1\}\) o \(\{0, 1\}\) dependiendo de la utilidad en la formulación del problema.
Veamos el caso más sencillo de clasificación en el escenario de clasificación binaria que conecta un poco con regresión lineal
Regresión Logística#
El modelo lineal#
Recordemos el caso de regresión donde la función \(f\) es:
siendo \(X \in \mathbb{R}^{n, p}\) nuestro conjunto de datos que denominamos matriz de datos
La solución cerrada (ecuaciones normales) para conseguir el mejor modelo para \(\beta \in \mathbb{R}^p\) es: $\(\beta^* = (X^T X)^{-1}X^Ty\)$
siendo \(y \in \mathbb{R}^n \) el vector de respuestas de nuestro dataset \((X, y)\)
Discusión#
Cómo podríamos clasicar datos asumiendo que el setup:
Matriz de datos \(X\)
la variable a predecir es \(y \in \{0, 1\}\)
Para simplificar la idea, asumamos que \(X \in \mathbb{R}\)
Colocar imágenes de discusión
#@ plot_curve(f, _params=[], _range=(-5, 5), _points=100)
import matplotlib.pyplot as plt
def plot_curve(f, _params=[], _range=(-5, 5), _points=100):
"""
Método para graficar una curva f(x) cuyos parámetros fijos son _params en el rango _range(min, max) usando subsampling de _points
:param f: La función a graficar
:param _params: Los parámetros fijos de la función
:param _range: El rango de X (min, max)
:param _points: Número de puntos donde vamos a subsamplear a f
:returns: Nada
"""
X = np.linspace(_range[0], _range[1], _points)
plt.plot(X, np.array(list(map(lambda x: f(x, *_params), X))))
Graficando la función logística#
La función logística#
Conocidad también como curva sigmoide:
Qué valores usaríamos nosotros?
import numpy as np
plot_curve(f, _params=[], _range=(-5, 5), _points=100):
f = lambda x, L, k, x0: L/(1.0 + np.exp(-1.0*k*(x-x0)))
def f(x, L, k, x0):
return L/(1.0 + np.exp(-1.0*k*(x-x0))
plot_curve(f, (1, 10, 0), _range=(-10, 10))
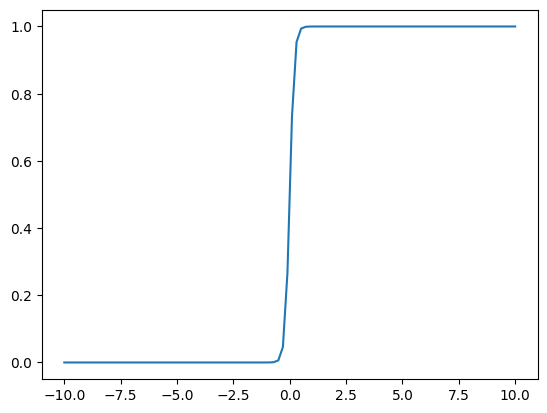
plot_curve(f, (1, 2, 0), _range=(-10, 10))
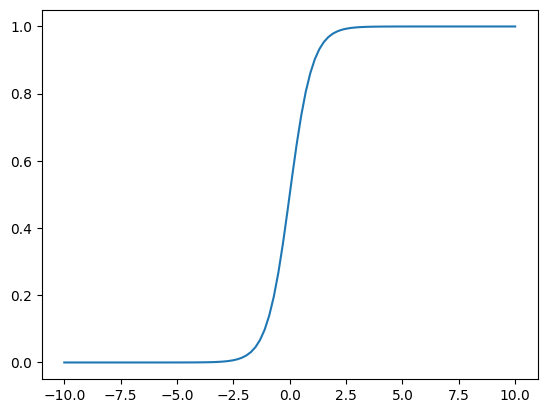
plot_curve(f, (5, 2, 6), _range=(-10, 10))
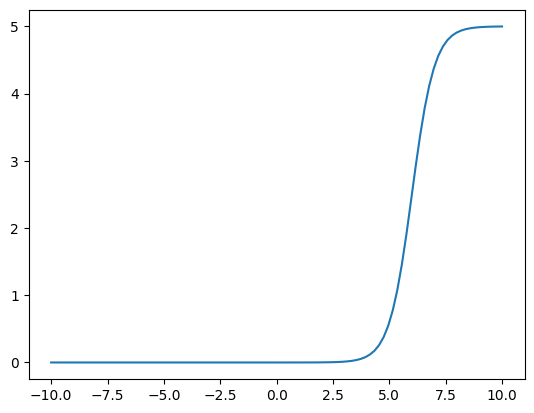
plot_curve(f, (5, 2, 6))
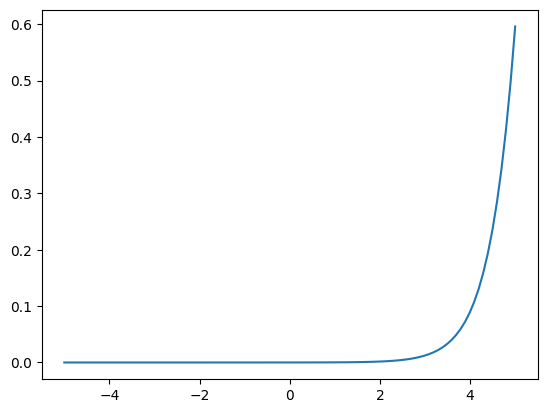
plot_curve(f, (1, 1, 0), _range=(-5, 5))
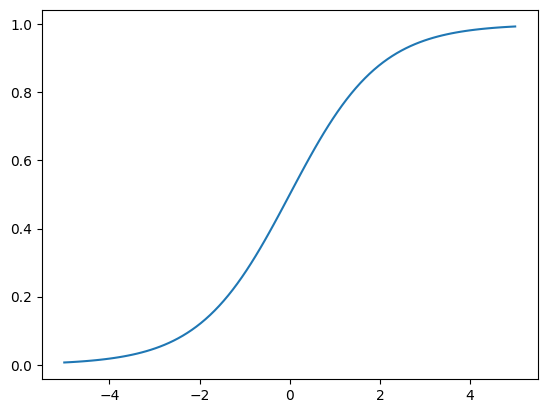
Scipy#
from scipy.stats import logistic
# logistic.cdf -> cummalitive density function
FDA
P(x<=X)
plot_curve(logistic.cdf)

El modelo logístico#
Supongamos que tenemos una matriz de datos \(X\) y la variable a predecir es \(y \in \{0, 1\}\)
En general, buscamos conseguir predecir la probabilidad de que una instancia de nuestro dataset \(x_i\) pertenezca a una categoría \(0\) o \(1\).
Si recordamos definición de probabilidad condicional, queremos \(P(y_i| x_i)\) para todo \(i\) en el dataset.
Asumamos por simplicidad que \(x_i\) es solo una columna.
Buscamos \(P(y_i=1 | x_i=a)\) y \(P(y_i=0 | x_i=a)\) para decidir si \(x_i\) pertenece a la clase \(1\) o \(0\), respectivamente.
El caso simple#
El caso simple para regresión logística
Cómo podemos reescribir la definición que tenemos? $\( f(x)=\frac{L}{1+e^{-k\left(x-x_0\right)}}\)$
Propiedad importante de f#
Con manipulaciones simples, podemos demostrar que:
Por lo que,
Esta forma es conocida como la transformación log odd o logit.
Tenemos f, quién es L?#
Usando la función de verosimilitud (likelihood) asumiendo independencia para cada instancia de \(X\) buscamos:
Esta probabilidad da la probabilidad de los ceros y unos observados en los datos. Elegimos \(\beta_0\) y \(\beta_1\) para maximizar la probabilidad de los datos observados.
Cuya representación algunas veces varía a:
Predicción#
Una vez que conseguimos el modelo óptimo \(\beta^*\), la predicción es:
Regresión Logística Múltiple#
Consideramos ahora el problema de predecir una clase binaria con múltiples predictores. Haciendo analogía y extendiendo la idea de regresión logística simple tenemos:
donde \(x=\left(x_1, \ldots, x_p\right)\) son los \(m\) predictores. Y la función de predicción es $\( f(x)=\frac{e^{x^T \beta^* }}{1+e^{x^T \beta^* }}=\frac{e^{\beta_0+\beta_1 x_1+\cdots+\beta_p x_p}}{1+e^{\beta_0+\beta_1 x_1+\cdots+\beta_p x_p}} . \)$
Usaremos el módulo LogisticRegression de Scikit-Learn
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
Caso binario#
X, y = load_iris(return_X_y=True)
X.shape
(150, 4)
y.shape
(150,)
y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
y > 0
array([False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True])
y = np.array(y>0).astype(int)
arr = []
for yi in y:
if yi == 0:
arr.append(0)
else:
arr.append(1)
np.array(arr)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
np.array([0 if yi==0 else 1 for yi in y])
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
# random_state -> "la semilla (seed) de los RNG (random number generators)" -> Reproducibilidad
model = LogisticRegression(max_iter=1000, random_state=0).fit(X, y)
# penalty = None -> No tener regularización, LASSO y Ridge.
model = LogisticRegression(random_state=0, max_iter=1000, penalty=None).fit(X, y)
model.predict(X[:2, :])
array([0, 0])
model.predict(X[:50, :])
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0])
X[:2, :]
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2]])
model.predict_proba(X[:1, :])
array([[9.99999996e-01, 3.94190051e-09]])
[0.99..9 0]
model.intercept_
array([-1.18494836])
model.coef_
array([[-2.02162242, -6.99849918, 11.14813559, 5.15488554]])
$$
Estamos haciendo los mismos cálculos?#
X[:1, :] @ model.coef_[0]
array([-18.16665451])
X[:1, :] @ model.coef_[0] + model.intercept_
array([-19.35160286])
np.exp(X[:1, :] @ model.coef_[0] + model.intercept_)
array([3.94190053e-09])
Ahora tenemos 4 parámetros por columna _coef más el punto de corte intercept
np.exp(X[:1, :] @ model.coef_[0] + model.intercept_) / (1 + np.exp(X[:1, :] @ model.coef_[0] + model.intercept_))
array([3.94190051e-09])
np.array([1.0]) - np.exp(X[:1, :] @ model.coef_[0] + model.intercept_) / (1 + np.exp(X[:1, :] @ model.coef_[0] + model.intercept_))
array([1.])
Caso Multinomial#
Es posible extender la definición para casos con más de 1 clase y además con \(m>1\)
Asumamos que \(|C| = K\)
para \(k=1, \ldots, K-1\), y $\( \operatorname{Pr}(y=K \mid X=x)=\frac{1}{1+\sum_{l=1}^{K-1} e^{\beta_{l 0}+\beta_{l 1} x_1+\cdots+\beta_{l m} x_m}} . \)$
No es difícil probar que: \(k=1, \ldots, K-1\), $\( \log \left(\frac{\operatorname{Pr}(y=k \mid X=x)}{\operatorname{Pr}(Y=K \mid X=x)}\right)=\beta_{k 0}+\beta_{k 1} x_1+\cdots+\beta_{k m} x_m \)$
X, y = load_iris(return_X_y=True)
X[:2, :]
array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2]])
model = LogisticRegression(random_state=0, max_iter=10000, penalty=None, multi_class="multinomial").fit(X, y)
model.predict(X[:2, :])
array([0, 0])
model.predict_proba(X[:2, :])
array([[1.00000000e+00, 2.09745715e-31, 3.23880813e-58],
[1.00000000e+00, 1.23379546e-24, 8.80642052e-50]])
model.score(X, y)
0.9866666666666667
model.intercept_
array([ 3.97751891, 19.33028473, -23.30780364])
model.coef_
array([[ 7.35275466, 20.39784579, -30.26354695, -14.14340745],
[ -2.44378438, -6.85846875, 10.41707167, -2.07137781],
[ -4.90897028, -13.53937704, 19.84647528, 16.21478526]])