Pizarra#
from tldraw import TldrawWidget
t = TldrawWidget(width=1502, height = 700)
t
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 from tldraw import TldrawWidget
2 t = TldrawWidget(width=1502, height = 700)
3 t
ModuleNotFoundError: No module named 'tldraw'
Cálculos para el punto de corte
Cálculos para la pendiente
Tarea: Demostrar que (2) es equivalente a la expresión que derivamos
Pregunta interesante: Aumentando la complejidad (grado del polinomio) de la solución
Por qué es mínimo y propiedades de X
!pip install tldraw
Collecting tldraw
Downloading tldraw-2.0.14-py2.py3-none-any.whl (3.6 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 3.6/3.6 MB 30.6 MB/s eta 0:00:00
?25hCollecting anywidget (from tldraw)
Downloading anywidget-0.9.11-py3-none-any.whl (248 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 248.4/248.4 kB 24.7 MB/s eta 0:00:00
?25hRequirement already satisfied: ipykernel in /usr/local/lib/python3.10/dist-packages (from tldraw) (5.5.6)
Collecting ipylab (from tldraw)
Downloading ipylab-1.0.0-py3-none-any.whl (100 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 100.2/100.2 kB 10.5 MB/s eta 0:00:00
?25hRequirement already satisfied: requests in /usr/local/lib/python3.10/dist-packages (from tldraw) (2.31.0)
Requirement already satisfied: ipywidgets>=7.6.0 in /usr/local/lib/python3.10/dist-packages (from anywidget->tldraw) (7.7.1)
Collecting psygnal>=0.8.1 (from anywidget->tldraw)
Downloading psygnal-0.11.1-cp310-cp310-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (727 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 727.4/727.4 kB 34.6 MB/s eta 0:00:00
?25hRequirement already satisfied: typing-extensions>=4.2.0 in /usr/local/lib/python3.10/dist-packages (from anywidget->tldraw) (4.11.0)
Requirement already satisfied: ipython-genutils in /usr/local/lib/python3.10/dist-packages (from ipykernel->tldraw) (0.2.0)
Requirement already satisfied: ipython>=5.0.0 in /usr/local/lib/python3.10/dist-packages (from ipykernel->tldraw) (7.34.0)
Requirement already satisfied: traitlets>=4.1.0 in /usr/local/lib/python3.10/dist-packages (from ipykernel->tldraw) (5.7.1)
Requirement already satisfied: jupyter-client in /usr/local/lib/python3.10/dist-packages (from ipykernel->tldraw) (6.1.12)
Requirement already satisfied: tornado>=4.2 in /usr/local/lib/python3.10/dist-packages (from ipykernel->tldraw) (6.3.3)
Requirement already satisfied: charset-normalizer<4,>=2 in /usr/local/lib/python3.10/dist-packages (from requests->tldraw) (3.3.2)
Requirement already satisfied: idna<4,>=2.5 in /usr/local/lib/python3.10/dist-packages (from requests->tldraw) (3.7)
Requirement already satisfied: urllib3<3,>=1.21.1 in /usr/local/lib/python3.10/dist-packages (from requests->tldraw) (2.0.7)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.10/dist-packages (from requests->tldraw) (2024.2.2)
Requirement already satisfied: setuptools>=18.5 in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (67.7.2)
Collecting jedi>=0.16 (from ipython>=5.0.0->ipykernel->tldraw)
Downloading jedi-0.19.1-py2.py3-none-any.whl (1.6 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.6/1.6 MB 36.5 MB/s eta 0:00:00
?25hRequirement already satisfied: decorator in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (4.4.2)
Requirement already satisfied: pickleshare in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (0.7.5)
Requirement already satisfied: prompt-toolkit!=3.0.0,!=3.0.1,<3.1.0,>=2.0.0 in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (3.0.43)
Requirement already satisfied: pygments in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (2.16.1)
Requirement already satisfied: backcall in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (0.2.0)
Requirement already satisfied: matplotlib-inline in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (0.1.7)
Requirement already satisfied: pexpect>4.3 in /usr/local/lib/python3.10/dist-packages (from ipython>=5.0.0->ipykernel->tldraw) (4.9.0)
Requirement already satisfied: widgetsnbextension~=3.6.0 in /usr/local/lib/python3.10/dist-packages (from ipywidgets>=7.6.0->anywidget->tldraw) (3.6.6)
Requirement already satisfied: jupyterlab-widgets>=1.0.0 in /usr/local/lib/python3.10/dist-packages (from ipywidgets>=7.6.0->anywidget->tldraw) (3.0.10)
Requirement already satisfied: jupyter-core>=4.6.0 in /usr/local/lib/python3.10/dist-packages (from jupyter-client->ipykernel->tldraw) (5.7.2)
Requirement already satisfied: pyzmq>=13 in /usr/local/lib/python3.10/dist-packages (from jupyter-client->ipykernel->tldraw) (24.0.1)
Requirement already satisfied: python-dateutil>=2.1 in /usr/local/lib/python3.10/dist-packages (from jupyter-client->ipykernel->tldraw) (2.8.2)
Requirement already satisfied: parso<0.9.0,>=0.8.3 in /usr/local/lib/python3.10/dist-packages (from jedi>=0.16->ipython>=5.0.0->ipykernel->tldraw) (0.8.4)
Requirement already satisfied: platformdirs>=2.5 in /usr/local/lib/python3.10/dist-packages (from jupyter-core>=4.6.0->jupyter-client->ipykernel->tldraw) (4.2.2)
Requirement already satisfied: ptyprocess>=0.5 in /usr/local/lib/python3.10/dist-packages (from pexpect>4.3->ipython>=5.0.0->ipykernel->tldraw) (0.7.0)
Requirement already satisfied: wcwidth in /usr/local/lib/python3.10/dist-packages (from prompt-toolkit!=3.0.0,!=3.0.1,<3.1.0,>=2.0.0->ipython>=5.0.0->ipykernel->tldraw) (0.2.13)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.10/dist-packages (from python-dateutil>=2.1->jupyter-client->ipykernel->tldraw) (1.16.0)
Requirement already satisfied: notebook>=4.4.1 in /usr/local/lib/python3.10/dist-packages (from widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (6.5.5)
Requirement already satisfied: jinja2 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (3.1.4)
Requirement already satisfied: argon2-cffi in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (23.1.0)
Requirement already satisfied: nbformat in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (5.10.4)
Requirement already satisfied: nbconvert>=5 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (6.5.4)
Requirement already satisfied: nest-asyncio>=1.5 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.6.0)
Requirement already satisfied: Send2Trash>=1.8.0 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.8.3)
Requirement already satisfied: terminado>=0.8.3 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.18.1)
Requirement already satisfied: prometheus-client in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.20.0)
Requirement already satisfied: nbclassic>=0.4.7 in /usr/local/lib/python3.10/dist-packages (from notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.0.0)
Requirement already satisfied: jupyter-server>=1.8 in /usr/local/lib/python3.10/dist-packages (from nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.24.0)
Requirement already satisfied: notebook-shim>=0.2.3 in /usr/local/lib/python3.10/dist-packages (from nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.2.4)
Requirement already satisfied: lxml in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (4.9.4)
Requirement already satisfied: beautifulsoup4 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (4.12.3)
Requirement already satisfied: bleach in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (6.1.0)
Requirement already satisfied: defusedxml in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.7.1)
Requirement already satisfied: entrypoints>=0.2.2 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.4)
Requirement already satisfied: jupyterlab-pygments in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.3.0)
Requirement already satisfied: MarkupSafe>=2.0 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (2.1.5)
Requirement already satisfied: mistune<2,>=0.8.1 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.8.4)
Requirement already satisfied: nbclient>=0.5.0 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.10.0)
Requirement already satisfied: packaging in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (24.0)
Requirement already satisfied: pandocfilters>=1.4.1 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.5.1)
Requirement already satisfied: tinycss2 in /usr/local/lib/python3.10/dist-packages (from nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.3.0)
Requirement already satisfied: fastjsonschema>=2.15 in /usr/local/lib/python3.10/dist-packages (from nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (2.19.1)
Requirement already satisfied: jsonschema>=2.6 in /usr/local/lib/python3.10/dist-packages (from nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (4.19.2)
Requirement already satisfied: argon2-cffi-bindings in /usr/local/lib/python3.10/dist-packages (from argon2-cffi->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (21.2.0)
Requirement already satisfied: attrs>=22.2.0 in /usr/local/lib/python3.10/dist-packages (from jsonschema>=2.6->nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (23.2.0)
Requirement already satisfied: jsonschema-specifications>=2023.03.6 in /usr/local/lib/python3.10/dist-packages (from jsonschema>=2.6->nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (2023.12.1)
Requirement already satisfied: referencing>=0.28.4 in /usr/local/lib/python3.10/dist-packages (from jsonschema>=2.6->nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.35.1)
Requirement already satisfied: rpds-py>=0.7.1 in /usr/local/lib/python3.10/dist-packages (from jsonschema>=2.6->nbformat->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.18.1)
Requirement already satisfied: anyio<4,>=3.1.0 in /usr/local/lib/python3.10/dist-packages (from jupyter-server>=1.8->nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (3.7.1)
Requirement already satisfied: websocket-client in /usr/local/lib/python3.10/dist-packages (from jupyter-server>=1.8->nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.8.0)
Requirement already satisfied: cffi>=1.0.1 in /usr/local/lib/python3.10/dist-packages (from argon2-cffi-bindings->argon2-cffi->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.16.0)
Requirement already satisfied: soupsieve>1.2 in /usr/local/lib/python3.10/dist-packages (from beautifulsoup4->nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (2.5)
Requirement already satisfied: webencodings in /usr/local/lib/python3.10/dist-packages (from bleach->nbconvert>=5->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (0.5.1)
Requirement already satisfied: sniffio>=1.1 in /usr/local/lib/python3.10/dist-packages (from anyio<4,>=3.1.0->jupyter-server>=1.8->nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.3.1)
Requirement already satisfied: exceptiongroup in /usr/local/lib/python3.10/dist-packages (from anyio<4,>=3.1.0->jupyter-server>=1.8->nbclassic>=0.4.7->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (1.2.1)
Requirement already satisfied: pycparser in /usr/local/lib/python3.10/dist-packages (from cffi>=1.0.1->argon2-cffi-bindings->argon2-cffi->notebook>=4.4.1->widgetsnbextension~=3.6.0->ipywidgets>=7.6.0->anywidget->tldraw) (2.22)
Installing collected packages: psygnal, jedi, ipylab, anywidget, tldraw
Successfully installed anywidget-0.9.11 ipylab-1.0.0 jedi-0.19.1 psygnal-0.11.1 tldraw-2.0.14
01 Regresión Lineal#
Derivando soluciones
Usando Scikit-Learn
Versión v.2#
El notebook lo puedo modificar, esta versión es la v.1 a 24/05/2024 a l pm de Caracas.
Autor: Fernando Crema García Contacto: fernando.cremagarcia@kuleuven.be; fernando.cremagarcia@esat.kuleuven.be
Regresión lineal#
Consideremos el problema de Regresión lineal : $\(y = \mathbf{X} \theta_* + \epsilon \text{ con }\)$
\(\mathbf{X} \in \mathbb{R}^{n,p}\) a nuestra matriz de datos.
\(\epsilon \in \mathbb{R}\) el ruido aleatorio definido como una variable aleatoria Normal con media \(0\) y varianza \(\sigma^2\), esto es, \(\epsilon \sim \mathcal{N}(\mu=0,\,\sigma^{2})\)
\(y \in \mathbb{R}^n\) es nuestro vector a predecir que llamamos comunmente vector respuesta y del cual asumimos una relación lineal con \(\mathbf{X}\).
\(\theta_* \in \mathbb{R}^m\) es el modelo óptimo.
Supongamos que tenemos una muestra aleatoria de (\(X, \mathbf{y}\)) de tamaño \(n\) para ambas \(\mathbf{X}\) y \(y\) entonces \(X \in \mathbb{R}^{n \times p}\) y \(\mathbf{y} \in \mathbb{R}^n\). El obketivo principal es conseguir \(\theta_*\).
Formulación de regresión lineal:#
El problema a resolver es:
Derivando las ecuaciones normales#
Solución analítica (Ecuaciones normales)#
Nuestro primer modelo#
import numpy as np
x = np.random.randn(10)
np.size(x)
10
ones = np.ones(10)
X = np.stack([x, ones], axis=1)
np.size(X)
20
X
array([[-0.8080633 , 1. ],
[-0.2500174 , 1. ],
[ 0.98161629, 1. ],
[-0.32656151, 1. ],
[-0.88471539, 1. ],
[ 1.65161928, 1. ],
[ 2.82752818, 1. ],
[-0.96407817, 1. ],
[ 0.48651643, 1. ],
[ 0.16247403, 1. ]])
np.matrix?
input_matrix = []
# Tuple
for xi, onesi in zip(x, ones):
input_matrix.append("{} {}".format(xi, onesi))
X = np.matrix(";".join(input_matrix))
X
matrix([[-0.8080633 , 1. ],
[-0.2500174 , 1. ],
[ 0.98161629, 1. ],
[-0.32656151, 1. ],
[-0.88471539, 1. ],
[ 1.65161928, 1. ],
[ 2.82752818, 1. ],
[-0.96407817, 1. ],
[ 0.48651643, 1. ],
[ 0.16247403, 1. ]])
X
matrix([[ 0.21262992, 1. ],
[-1.4821317 , 1. ],
[-0.02905379, 1. ],
[-0.31234722, 1. ],
[ 0.05402455, 1. ],
[ 1.69872219, 1. ],
[ 2.37489091, 1. ],
[-0.74516778, 1. ],
[-1.31825004, 1. ],
[-1.46539355, 1. ]])
Modelo teórico#
beta_star = np.array([2.0, 3.0])
y = np.dot(X, beta_star)
y
matrix([[1.3838734 , 2.4999652 , 4.96323258, 2.34687698, 1.23056921,
6.30323856, 8.65505636, 1.07184366, 3.97303287, 3.32494805]])
y.size(
type(y)
numpy.matrix
viendo la componente \(y_1\)#
y[0][0] * 2.0 + 3.0
matrix([[ 5.7677468 , 7.9999304 , 12.92646515, 7.69375395, 5.46113842,
15.60647713, 20.31011272, 5.14368732, 10.94606574, 9.6498961 ]])
Buscar las soluciones usando las ecuaciones normales#
from numpy.linalg import inv as inversa
import pandas as pd
\(\beta_* = (X^T X)^{-1} X^{T} y \)
def ecuaciones_normales_no(X, y):
"""
:param X: La matriz de datos
:param y: El vector de observaciones
:returns: El vector beta estrella
"""
return np.dot(np.dot(inversa(np.dot(X.T, X), X.T, y)))
def ecuaciones_normales(X, y):
"""
:param X: La matriz de datos
:param y: El vector de observaciones
:returns: El vector beta estrella
"""
return inversa(X.T @ X) @ X.T @ y
X @ beta_star
matrix([[1.3838734 , 2.4999652 , 4.96323258, 2.34687698, 1.23056921,
6.30323856, 8.65505636, 1.07184366, 3.97303287, 3.32494805]])
Transpuesta#
np.transpose(X)
matrix([[-0.8080633 , -0.2500174 , 0.98161629, -0.32656151, -0.88471539,
1.65161928, 2.82752818, -0.96407817, 0.48651643, 0.16247403],
[ 1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ]])
X.T
matrix([[-0.8080633 , -0.2500174 , 0.98161629, -0.32656151, -0.88471539,
1.65161928, 2.82752818, -0.96407817, 0.48651643, 0.16247403],
[ 1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ]])
Probando el método#
beta_star
array([2., 3.])
y
matrix([[1.3838734 , 2.4999652 , 4.96323258, 2.34687698, 1.23056921,
6.30323856, 8.65505636, 1.07184366, 3.97303287, 3.32494805]])
y = y.reshape(10, 1)
X
matrix([[ 0.21262992, 1. ],
[-1.4821317 , 1. ],
[-0.02905379, 1. ],
[-0.31234722, 1. ],
[ 0.05402455, 1. ],
[ 1.69872219, 1. ],
[ 2.37489091, 1. ],
[-0.74516778, 1. ],
[-1.31825004, 1. ],
[-1.46539355, 1. ]])
ecuaciones_normales(X, y)
matrix([[2.],
[3.]])
import matplotlib.pyplot as plt
!pip install <paquete>
beta_star = beta_star.reshape(2, 1)
plt.plot(X[:, 0], X @ beta_star, X[:, 0], y, 'o')
[<matplotlib.lines.Line2D at 0x7dfaf2e77790>,
<matplotlib.lines.Line2D at 0x7dfaf2e00880>]
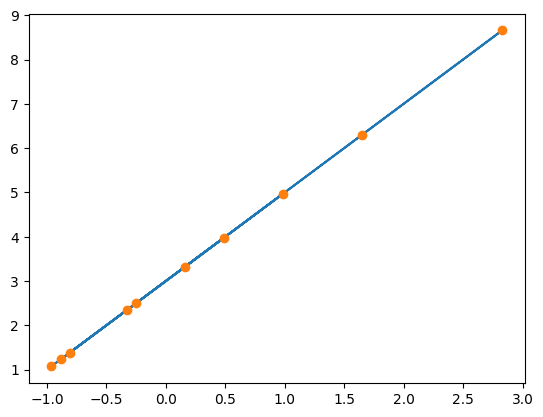
Agregando ruido#
# np.random.randn ~ N(0, 1) en clases vimos que el ruido N(0, sigma)
# Las columnas ahora siguen Y = 30 X + 10 + ruido
X = np.stack([np.random.randn(1000), np.ones(1000)], axis=1)
X
array([[-1.07445498, 1. ],
[ 2.26035941, 1. ],
[ 0.05507815, 1. ],
...,
[-0.22494241, 1. ],
[-1.87232309, 1. ],
[-0.57393463, 1. ]])
beta = np.array([30, 10])
Sobrecarga de operadores#
np.random.randn() -> un valor en R lo multiplico por 5
y = X @ beta + 5*np.random.randn(1000)
y
beta_star_nuevo = ecuaciones_normales(X, y)
beta_star_nuevo
array([29.93435641, 9.91365681])
plt.plot( X[:, 0], y, 'o', X[:, 0], X @ beta_star_nuevo)
[<matplotlib.lines.Line2D at 0x7dfaf0b98df0>,
<matplotlib.lines.Line2D at 0x7dfaf0b98eb0>]
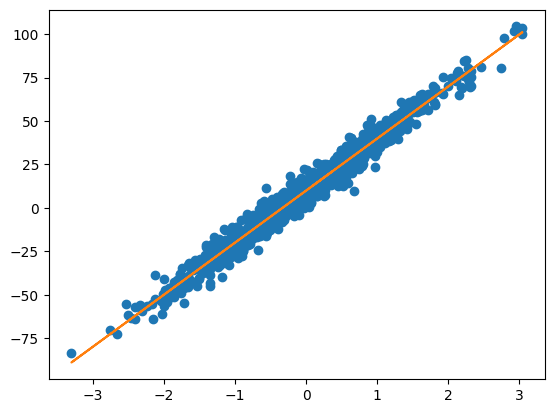
from sklearn.linear_model import LinearRegression
En general, todos los objetos (names) de SK Learn tienen asociado el método fit (entrenar). Si es un problema de regresión o de clasificación buscamos \(f(X) = y\) como tenemos nuestros datos \(X\) y el vector de salidas \(y\) el método siempre recibe ambas en ese orden.
model = LinearRegression().fit(X, y)
Tres opciones para generar el modelo usando SK Learn#
# Abre un menu al lado derecho con métodos, parámetros y ejemplos de uso del modelo
model?
coef_ siempre tendrá los parámetros entrenamos de \(\beta\) SIN el punto de corte
model.coef_
array([29.93435641, 0. ])
el punto de corte que en clases hemos llamado \(\beta_0\) está en intercept_
model.intercept_
10.027010864725078
La primera manera de entrenar es agregando la columna de 1s y quitando el intercept
model1 = LinearRegression(fit_intercept=False).fit(X, y)
model1.coef_
array([29.99734383, 10.02701086])
model1.intercept_
0.0
La segunda manera de entrenar es usando solamente los datos relevantes (columna sin 1s) y el intercept tendrá el punto de corte porque fit_intercept no es False
model3 = LinearRegression().fit(X[:, 0].reshape(1000, 1), y)
model3.coef_
array([29.93435641])
model3.intercept_
9.913656812204634
Por último, el \(\beta^*\) lo podemos crear concatenando ambos valores. Sin embargo, TAREA: existe una manera de obtener el modelo como parámetro.
beta_star_scikit = np.array([model3.coef_[0], model3.intercept_])
beta_star_scikit
array([29.99734383, 10.02701086])
Nos da el mismo modelo que usando las ecuaciones normales
array([29.99734383, 10.02701086])
Comentarios#
No nos da 30, 10 exactamente por el ruido asociado.
Si el ruido asociado sigue N(0, sigma) entonces regresión lineal debería funcionar bien
Si el ruido asociado NO es normal, no va a funcionar bien.
Cómo sabemos que un modelo “es bueno”?#
Gráfico tomado de Coefficient of determination
De donde $\(\color{blue}{S S_{\mathrm{res}}} = \sum_i\left(y_i-f(x_i)\right)^2=\sum_i e_i^2 \)\( y \)\(\color{red}{S S_{\mathrm{tot}}} = S S_{\mathrm{tot}}=\sum_i\left(y_i-\bar{y}\right)^2 \)$
Vean como el denominador es constante para todos los posibles modelos!
Cuáles son los posibles valores de \(R^2\)